Well, here is the short story: RF Spectrum Analyzers display the result in dBm, whereas noise specifications are often given in nV/sqrt(Hz).
So, all we need is a conversion between those units, right? If you just want the answer, here it is:
| RF Power | Noise Density |
|---|---|
| [dBm] | [nV/sqrt(Hz)] |
| -80 | 223 |
| -90 | 70.7 |
| -100 | 22.3 |
| -110 | 7.07 |
| -120 | 2.23 |
The above table works if your spectrum analyzer input is terminated with 50 Ohms and you have set the spectrum analyzer to 10 kHz resolution bandwidth.
Background
I stumbled over this minor nuisance when simulating the noise performance of an RF amplifier. SPICE will produce a plot of the power density given in V/sqrt(Hz). When I wanted to compare the noise of the real circuit which I built, the spectrum analyzer could only display in dBm.
While it is absolutely common for a spectrum analyzer to use dBm as a unit, one must not forget that dBm is an absolute measure for RF power. 0 dBm is 1 mW. However, when dealing with a noise spectrum, the display is actually more like a Power Density rather than an absolute power level, since the spectrum analyzer is showing the power within a certain Resolution Bandwidth (e.g. 1MHz). You could read it like this: A reading of 0 dBm means there is an RF power of 1 mW within a spectral slice of 1MHz.
The Conversion
There is an implicit assumption in the spectrum analyzer readings. The assumption is that the power is dissipated in the termination resistor inside the instrument. You probably know that the inputs are terminated with 50 Ohms (most of them are anyway). A DC voltage of 1V will thus dissipate 20mW (P=V^2/R). This is the reason why we need to know the termination resistance Rterm to convert an RF power to a voltage. We also need to know the resolution bandwidth RBW (in Hz) the spectrum analyzer is using. To convert, we basically convert dBm into Watts. Then we divide by the resolution bandwidth in order to find out how much power is in one Hz. Then we convert into Volts using the termination resistor.
This is the formula for the Noise Density n:
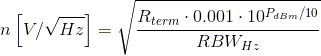
Total Noise Level
But what can we do with the Noise Density n? Well, the reason why I needed it was to find out about the smallest reading my circuit can reliably measure. The “Noise” in the Signal-To-Noise ratio can easily be calculated when you have the Noise Density of your circuit. All you need is the bandwidth of your circuit. Let’s say your circuit has a bandwidth of 100MHz and the measured noise level is -100dBm according to the spectrum analyzer. Then the noise density is 22.3nV/sqrt(Hz), multiplied with sqrt(100e6 Hz) we get a total noise of 223 uVrms.
RMS (Root-Mean-Square) values are often used in RF. If we assume white noise, you can multiply by 6.6 to get the peak-to-peak variation (some use a factor of 8). That means we can expect to see a total noise of 1.34 mVpk-pk if we would measure with an oscilloscope.
Here is the formula:
![]()
Hints
- Set the RBW to “Manual” and choose 10kHz. Otherwise the spectrum analyzer will choose whatever it thinks is suitable for your start/stop frequency.
- Turn on the pre-amplifier. Chances are that your circuit has low noise. In my case, I had to manually enable the pre-amp.
- Run a control measurement with nothing connected to the spectrum analyzer. The internal noise of the spectrum analyzer should be lower than the noise you expect to measure.